2015-07-04

Pragmatic physically based rendering : Setup & Gamma

This blog post is a part of series about implementing PBR in WebGL from scratch:

  1. Intro
  2. Setup & Gamma

Updates

2015/09/03 Removed gamma correction for input param colors and assuming they are in the linear space already

2015/09/22 Reversed back to gamma input colors based on the discussion here https://github.com/mrdoob/three.js/issues/5838

Setup

Before we start let's make sure we can get the code up and running properly. I will assume you have working knowledge of JavaScript and GLSL.

NodeJS

Hopefully you also used nodejs and npm (node package manager) before as we will use it quite a lot here. If you don't have nodejs you should install it now from https://nodejs.org (this will also install npm for you)

Browser & OS

I'm testing all the code in Safari 8.0.7 (as of time of writing this blog post) on OSX 10.10.4. Most of the code should work in any other major browser (Chrome 43+, Firefox 39+, Safari 8+) and operating system. There are some extensions missing in Safari and Firefox that we will use for specific tasks but I'll always give a warning about it in the related section of each post. Making it work on mobile is not a top priority at the moment but I'll test it as much as I can on the iOS. I don't have an Android device to test with unfortunately (bug fixes and pull requests are welcome!).

Getting the code

All the code and text for these tutorials lives at https://github.com/vorg/pragmatic-pbr. You can get it by downloading master.zip or via git.

git clone https://github.com/vorg/pragmatic-pbr.git

Next let's enter the repo folder and install the dependencies.

cd pragmatic-pbr
npm install

Running the code

To make sure everything works run the following command while in pragmatic-pbr directory.

beefy 201-init/main.js --open --live -- -i plask -g glslify-promise/transform

This should open your browser at http://127.0.0.1:9966 and display a rectangle that changes colors


click to see the live version in a separate window

What is beefy? Beefy is a local server that bundles our code and required node modules into one JS file using browserify that can be loaded by the browser. It also watches for changes (when run with --live flag) and will reload the page when you edit and save the JS file. Running a local server also solves a number of issues with AJAX requests and local file access policies in the browsers. In the -- -i plask part we have browserify flags where we ignore plask module and run our source code through glslify transform that will inline all the GLSL shaders. Plask is a multimedia programming environment for OSX built on top of NodeJS and implementing WebGL v1.0+ spec. You can use it to run WebGL apps on OSX without the browser. I use it for development but we won't be using it in this tutorial.

Deploying the code

If you build on top of this tutorial and would like to have standalone (bundled) version that doesn't need beefy to run you can run the browserify yourself:

browserify 201-init/main.js -i plask -g glslify-promise/transform -o 201-init/main.web.js

You will then need to add following 201-init/index.html file:




    
    Pragmatic PBR

Dependencies

Pex

When I said 'from scratch' I was relating to modern rendering and PBR specific techniques. We don't want to reinvent the wheel and implement things like texture loading and creating WebGL context. For these boring parts we will be using pex. PEX is a WebGL library standing somewhere between stack.gl micromodules and monolithic three.js (although they started upgrading to a more modular code recently). This project is using next version of pex that's currently in development. There are numerous differences between this version and the one currently on npm:

As this version of pex is not on npm yet (the beauty of always alpha software) so we will require it straight from the GitHub. This is not a problem for npm. All we need to do is put the username (variablestudio is an org name for my studio variable.io before the package name in package.json where all the dependencies are specified and installed when calling npm install.

"dependencies": {
    "pex-cam": "variablestudio/pex-cam",
    "pex-context": "variablestudio/pex-context",
    "pex-io": "variablestudio/pex-io",
    "pex-math": "variablestudio/pex-math",
    "pex-sys": "variablestudio/pex-sys"
}
3rd party dependencies

We will use modules available on npm whenever possible for both JavaScript (e.g re-map) and GLSL via glslify (e.g. glsl-inverse)

Local dependencies

Recently I've started a new practice of extracting reusable code into micromodules as soon as possible in the project to prevent them from capturing too much context and becoming part of the spaghetti that every projects ends up in eventually (especially with last minute fixes). I put them in the local_modules folder and require as usual:

var createCube   = require('../local_modules/primitive-cube');

Most of them will eventually end up on npm but I want to make sure the API is tested in practice so we avoid v0.0.0 zombie modules that are abandoned after the first push (npm is full of them unfortunately).

201-init

This is just a quick test to make sure our setup works. The basic structure of a pex program is as follows (we will go into more details in the next section):

//imports
var Window = require('pex-sys/Window');

//Open window
Window.create({
    settings: {
        //initial window properties
    },
    resources: {
        //optional resource files to load before init
    },
    init: function() {
        //this code is executed after WebGL context creation
    },
    draw: function() {
        //this code is executed every frame
    }
})

So to make a window with background color changing every frame we would write:

var Window = require('pex-sys/Window');

var frame = 0;

Window.create({
    settings: {
        width: 1024,
        height: 576
    },
    //skipping resources
    //skipping init
    draw: function() {
        var ctx = this.getContext();
        frame++;
        var r = 0.5 + 0.5 * Math.sin(frame/10);
        var g = 0.5 + 0.5 * Math.cos(frame/10 + Math.PI/2);
        var b = 0.5 + 0.5 * Math.sin(frame/10 + Math.PI/4);
        ctx.setClearColor(r, g, b, 1.0);
        ctx.clear(ctx.COLOR_BIT);
    }
})

202-lambert-diffuse


click to see the live version in a separate window

Let's start with a simple scene containing one sphere and a single point light. We will make a number of assumptions: the surface of the sphere is white, the light color is white and there is no light attenuation (light loosing intensity with distance) and the light's position is static (no animation) and located at [10,10,10] (top right, in front of the sphere).

Diffuse Lighting

In order to calculate the appearance of a surface under these lighting conditions we need a lighting (shading) model. One of the simplest and most commonly used shading models is Lambertian reflectance also known as Lambert diffuse or just Lambert. It models a diffuse reflection (light reflecting into multiple directions -> blurry reflection) for matte / rough objects. It doesn't handle specular reflection (light reflecting into single direction causing -> sharp, mirror / highlight like) but we don't need that yet. Lambert diffuse obeys Lambert's cosine law stating that light intensity observed on the surface is proportional to the cosine of the angle between direction towards the light and the surface normal.

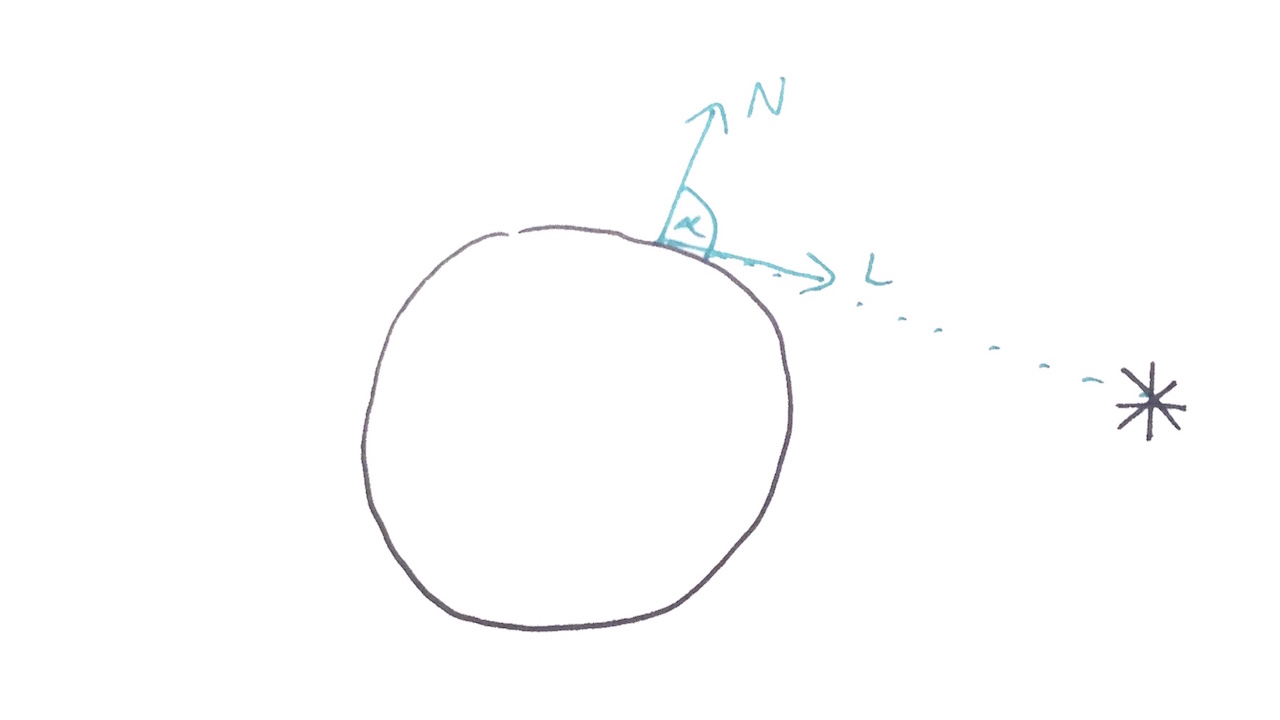
If both direction towards the light and normal point in the same direction the angle will be 0 and cos(0) = 1 therefore intensity will be the strongest. At 45' deg we have are losing 30% of the intensity cos(PI/4) = 0.707, dropping to zero at 90' deg as cos(PI/2) = 0.

We can measure the angle between two vectors using a dot productsN·L

//Id - diffuse intensity
Id = N·L

One way to calculate a dot product is to multiply lengths of the two vectors and cosine of the angle between them.

//|N| - length of the surface normal
//|L| - length of the direction towards the light
Id = N·L = |N|*|L|*cos(a)

If both the vectors are normalized (their length is 1) then our formula simplifies even more.

//assuming |N| = 1 and |L| = 1
Id = N·L = |N|*|L|*cos(a) = cos(a)

In practice we will always assume that input vectors N and L are normalized and use dot function that is natively supported in GLSL shader language.

I = dot(N, L)

Here is the implementation from glsl-diffuse-lambert module that we will later use.

glsl-diffuse-lambert/index.js:

float lambertDiffuse(vec3 lightDirection, vec3 surfaceNormal) {
  return max(0.0, dot(lightDirection, surfaceNormal));
}

The max(0.0, dot(L, N) is to prevent going below zero for angles > 90'deg that would cause invalid colors on the output (we can't go blacker than black [0,0,0]).

Transformations

In order to calculate dot product for each pixel of our sphere we first need to transform it's vertices in a Vertex Shader. This is a good place to talk about transformation spaces as different parts of shading are calculated in different spaces depending where is your data (e.g. you might calculate specular reflections from light in eye space as they are depending on viewer's position but environmental reflections in the world space where your skybox/environment is located).

We start in the model space with our sphere vertices. Model space is relative to the model itself i.e. point [0,0,0] will be usually in the center of the mesh (for a sphere) or at the bottom (for a standing person). By encoding mesh position, rotation and scale into a model matrix we can transform the vertices into world space - it's relative position to the center of the scene. In this example the sphere is centered so there is no transformations applied. Next we use camera position and direction to build view matrix that moves the vertices into the view space - position relative to the camera point of view. Projection matrix moves the vertices into projection space. This step will cause shapes far away from the camera appear smaller if we use perspective projection. Finally WebGL will then take the projected vertices no in so called normalized device coordinates, clip them (remove stuff outside of the screen) and calculate their final position relatively to the window based on the current viewport.

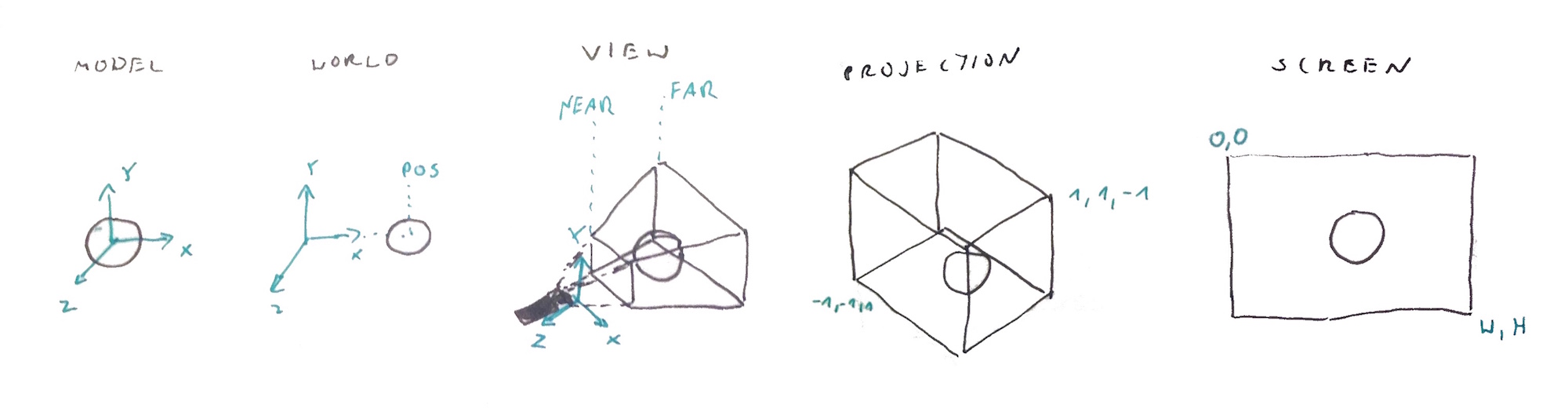
To clarify and sum up:

Model Space        //vertex position
     ↓
Model Matrix       //model position, rotation, scale
     ↓
World Space        //position in the scene
     ↓
View Matrix        //camera position and direction
     ↓
View Space         //eye space, camera space
     ↓
Projection Matrix  //perspective projection, orthographic projection
     ↓
Projection Space   //projection/ clipping space, normalized device coordinates
     ↓
  Viewport         //part of the window that we render to
     ↓
Screen Space       //window position

Here is the vertex shader we will use to do the job:

202-lambert-diffuse/Material.vert:

//vertex position in the model space
attribute vec4 aPosition;
//vertex normal in the model space
attribute vec3 aNormal;

//current transformation matrices coming from Context
uniform mat4 uProjectionMatrix;
uniform mat4 uViewMatrix;
uniform mat4 uModelMatrix;
uniform mat3 uNormalMatrix;

//user supplied light position
uniform vec3 uLightPos;

//vertex position in the eye coordinates (view space)
varying vec3 ecPosition;
//normal in the eye coordinates (view space)
varying vec3 ecNormal;
//light position in the eye coordinates (view space)
varying vec3 ecLightPos;

void main() {
    //transform vertex into the eye space
    vec4 pos = uViewMatrix * uModelMatrix * aPosition;
    ecPosition = pos.xyz;
    ecNormal = uNormalMatrix * aNormal;

    ecLightPos = vec3(uViewMatrix * uModelMatrix * vec4(uLightPos, 1.0));

    //project the vertex, the rest is handled by WebGL
    gl_Position = uProjectionMatrix * pos;
}

Notes:

You can read more about the math behind these matrices at Coding Labs: World, View and Projection Transformation Matrices.

Shading

Now that we are in the right transformation space and have all the data we can calculate the lambert diffuse for each pixel.

202-lambert-diffuse/Material.frag:

//require the lambert diffuse formula from a module via glslify
#pragma glslify: lambert   = require(glsl-diffuse-lambert)

//vertex position, normal and light position in the eye/view space
varying vec3 ecPosition;
varying vec3 ecNormal;
varying vec3 ecLightPos;

void main() {
     //normalize the normal, we do it here instead of vertex
     //shader for smoother gradients
    vec3 N = normalize(ecNormal);

    //calculate direction towards the light
    vec3 L = normalize(ecLightPos - ecPosition);

    //diffuse intensity
    float Id = lambert(L, N);

     //surface and light color, full white
    vec4 baseColor = vec4(1.0);
    vec4 lightColor = vec4(1.0);

    vec4 finalColor = vec4(baseColor.rgb * lightColor.rgb * Id, 1.0);
    gl_FragColor = finalColor;
}

Putting it all together

The last thing we need to do is to actually create the geometry, load the shaders, and render everything on the screen.

202-lambert-diffuse/main.js:

//Import all the dependencies
var Window       = require('pex-sys/Window');
var Mat4         = require('pex-math/Mat4');
var Vec3         = require('pex-math/Vec3');
var glslify      = require('glslify-promise');
var createSphere = require('primitive-sphere');

//Create window - in the borwser this will:
//- create new Canvas element with width/height specified in the `settings`
//- append it to 
//- get WebGL context
//- add event listeners for mouse and keyboard events
//- load all requested resources
//- call init()
//- keep calling draw() using Window.requestAnimationFrame()
Window.create({
    //Window / canvas properties
    settings: {
        width: 1024,
        height: 576
    },
    //Files (text, json, glsl vis glslify, images) to load before init
    resources: {
        vert: { glsl: glslify(__dirname + '/Material.vert') },
        frag: { glsl: glslify(__dirname + '/Material.frag') }
    },
    //Init is called after creating WebGL context and successfuly loading all the resources
    init: function() {
        //pex-context/Context object - the pex's WebGL context wrapper
        var ctx = this.getContext();

        //Model transformation matrix
        //An Array with 16 numbers initialized to an identity matrix
        this.model = Mat4.create();

        //Camera projection matrix
        this.projection = Mat4.perspective(
            Mat4.create(),             //new matrix
            45,                        //45' deg fov
            this.getAspectRatio(),     //window aspect ratio width/height
            0.001,                     //near clipping plane
            10.0                       //far clipping plane
        );

        //Camera view matrix
        this.view = Mat4.create();
        //[0,1,5] - eye position
        //[0,0,0] - target position
        //[0,1,0] - camera up vector
        Mat4.lookAt(this.view, [0, 1, 5], [0, 0, 0], [0, 1, 0]);

        //The Context keeps a separate matrix stack for the projection,
        //view and model matrix. Additionaly it will compute normal matrix
        //and inverse view matrix whenever view matrix changes
        ctx.setProjectionMatrix(this.projection);
        ctx.setViewMatrix(this.view);
        ctx.setModelMatrix(this.model);

        //Get reference to all loaded resources
        var res = this.getResources();

        //Each resource of type `glsl` will be replace by string with the loaded GLSL code
        //We can use that code to create a WebGL Program object
        this.program = ctx.createProgram(res.vert, res.frag);

        //Create sphere geometry - an object with positions, normals and cells/faces
        var g = createSphere();

        //Define mesh attribute layout
        //ATTRIB_POSITION and ATTRIB_NORMAL are slot numbers
        //matching attributes in the shader aPosition and aNormal
        var attributes = [
            { data: g.positions, location: ctx.ATTRIB_POSITION },
            { data: g.normals, location: ctx.ATTRIB_NORMAL }
        ];

        //Define vertices data
        var indices = { data: g.cells };

        //Create mesh to be rendered as a list of TRIANGLEs
        this.mesh = ctx.createMesh(attributes, indices, ctx.TRIANGLES);
    },
    //This function is called as close as possible to 60fps via requestAnimationFrame
    draw: function() {
        var ctx = this.getContext();

        //Set gl clear color to dark grey
        ctx.setClearColor(0.2, 0.2, 0.2, 1);

        //Clear the color and depth buffers
        ctx.clear(ctx.COLOR_BIT | ctx.DEPTH_BIT);

        //Enable depth testing
        ctx.setDepthTest(true);

        //Activate our GLSL program
        ctx.bindProgram(this.program);

        //Set the light's position uniform
        //There is no need to set matrix uniforms like uProjectionMatrix as
        //these are handled by the context. List of all handled uniforms is
        //in pex-context/ProgramUniform.js
        this.program.setUniform('uLightPos', [10, 10, 10])

        //Activate the sphere mesh
        ctx.bindMesh(this.mesh);

        //Draw the currently active mesh (sphere in this example)
        ctx.drawMesh();
    }
})

Running the code

Fire the following command to open this example in the browser:

beefy 202-lambert-diffuse/main.js --open --live -- -i plask -g glslify-promise/transform

203-gamma

PBR looks good because it's trying to avoid errors and approximations that accumulate across different rendering stages (color sampling, lighting / shading, blending etc). One of these assumptions is that that half the value 0.5 equals half the brightness. Unfortunately this is not how things work. Most screen we are using nowadays follow so called gamma curve that maps the input value to the brightness of a pixel in a non linear way.

Source: Wikipedia: Gamma_correction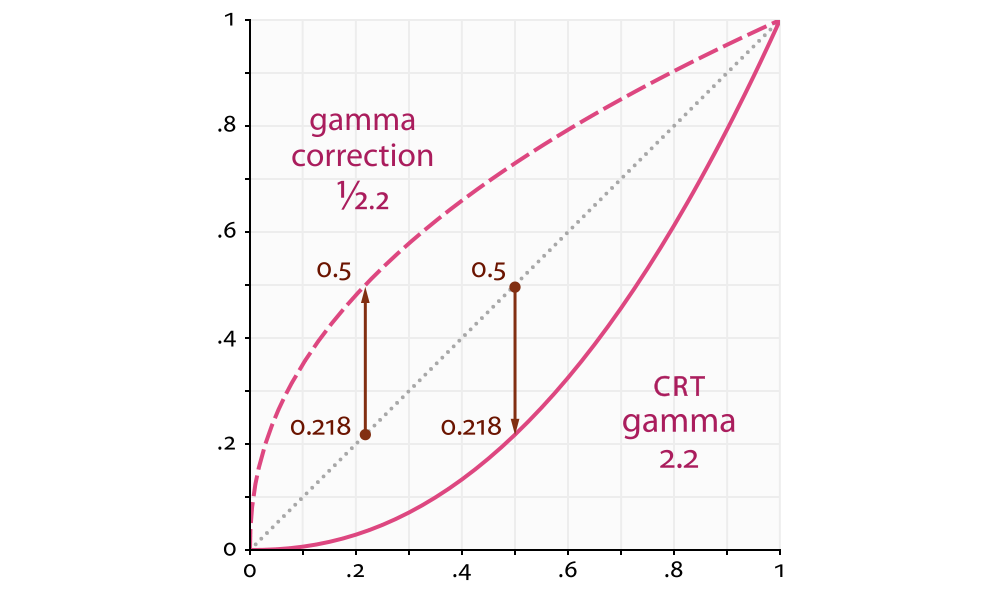

Because of historical reasons (cathode ray tube - CRT screens) whatever our application produces will be converted (made darker) by rising it to the power of 2.2. That value 2.2 is called gamma. This fact was often neglected to the medicare results and plastic look of older games.

At the same time most commonly used graphics formats like JPEG encode their colors using sRGB curve that negates this effect. I.e. They save values brighter that they are in reality (captured by the camera sensor). This also helps to keep more details (by using more bits) in the darker areas where human eyes are more sensitive. That sRGB curve negating the CRT gamma curve was the reason it all kind of worked so far, just the math was wrong so it was harder to achieve realistic (expected) results.

We will call these brighter color values gamma space and the unadjusted values linear space. You ALWAYS want to do your lighting calculations in the latter. Therefore whenever we get some color from a texture (unless it's linear data like HDR images) or another sRGB encoded value we need to convert it into linear space by rising to the power of 2.2 (0.45) and then after we are done we need to move it back to the gamma space by rising it to the power of 1.2/2.2. Monitor will then apply it's 2.2 curve and it all will look beautiful. Filmic Games: Linear-Space Lighting (i.e. Gamma) (2010) has great illustrations for that.

To sum up:

gamma space     //input colors
     ↓
pow(x, 2.2)     //(if in sRGB/gamma space)
     ↓
linear space    //do the lighting and blending math here
     ↓
pow(x, 1.0/2.2)
     ↓
gamma space     //colors for the screen

If you still feel confused (I would) please read more on the topic. Remember: Gamma / linear lighting is the "Number one trick to improve your rendering quality in no time!".

More reading:


click to see the live version in a separate window

203-gamma/Material.frag:

The vertex shader for is the same as for lambert diffuse. In the fragment shader we add the following lines:

//import gamma related functions
//glsl-gamma module exports two functions that we can import separately
#pragma glslify: toLinear = require(glsl-gamma/in)
#pragma glslify: toGamma  = require(glsl-gamma/out)

Now we can use them to obtain the correct color values to work with.

    //surface and light color, full white
    vec4 baseColor = toLinear(vec4(1.0)); //NEW
    vec4 lightColor = toLinear(vec4(1.0)); //NEW

     //lighting in the linear space
    vec4 finalColor = vec4(baseColor.rgb * lightColor.rgb * Id, 1.0);
    gl_FragColor = toGamma(finalColor);     //NEW
}

Note: using toLinear(vec4(1.0)) won't change much because pow(1, 2.2) is still 1 but this will become super important when we work with different colors and textures data.

Here is how toLinear and toGamma are implemented:

glsl-gamma/in:

const float gamma = 2.2;

vec3 toLinear(vec3 v) {
  return pow(v, vec3(gamma));
}

vec4 toLinear(vec4 v) {
  return vec4(toLinear(v.rgb), v.a);
}

glsl-gamma/out:

const float gamma = 2.2;

vec3 toGamma(vec3 v) {
  return pow(v, vec3(1.0 / gamma));
}

vec4 toGamma(vec4 v) {
  return vec4(toGamma(v.rgb), v.a);
}

The final code is in 203-gamma/Material.frag

To run the example:

beefy 203-gamma/main.js --open --live -- -i plask -g glslify-promise/transform

The final result looks pretty much like an object I've seen somewhere before... as Vincent Scheib is pointing on his Beautiful Pixels blog.

204-gamma-color

I know, I know. You are still not convinced. This video will change everything though:

I made a separate example with two lights for you to play with and see the results yourself:


click to see the live version in a separate window

To run the example:

beefy 204-gamma-color/main.js --open --live -- -i plask -g glslify-promise/transform

Try turning on/off the conversion to linear and gamma space to see the difference. Do you see that ugly brown on the left (uncorrected) side?

205-gamma-texture


click to see the live version in a separate window

Remember when I was talking about sRGB curves and textures? When using texture with sRGB encoded colors we need to bring them to the linear space as well:

vec4 baseColor = toLinear(texture2D(uAlbedoTex, vTexCoord0));

But first we need to create a texture in pex:

//define path to the assets directory, here it's above (..) the example
//folder so all examples can share the assets. `__dirname` is a nodejs
//built-in variable pointing to the folder where the js script lives,
//We need that to make it work in Plask.
var ASSETS_DIR = isBrowser ? '../assets' :  __dirname + '/../assets';

Then we declare the image resource to be loaded before init. texture is just a name we will use to refer to it later.

resources: {
   texture: { image: ASSETS_DIR + '/textures/Pink_tile_pxr128.jpg'}
},

Then in init() we can create the texture:

this.texture = ctx.createTexture2D(
  res.texture,
  res.texture.width,
  res.texture.height,
  { repeat: true }
);

And use it with the shader in draw():

ctx.bindTexture(this.texture, 0);
this.program.setUniform('uAlbedoTex', 0);

Why uAlbedoTex? Albedo is the base color reflected by the surface. In PBR it's preferred to the diffuseColor name as that would imply that lighting information is included in the texture data (e.g. imagine bricks with shadows in the cracks between them). Later we might use baseColor name which will be albedo color for diffuse materials but specular color for metals.

To run the example:

beefy 205-gamma-texture/main.js --open --live -- -i plask -g glslify-promise/transform

The brick texture comes from Pixar One Twenty Eight - a collection of classic textures from Pixar. Only some of them are suitable for physically based rendering as many include lighting / shadows baked together with color but you can find some nice stuff there:

206-gamma-ext-srgb

Decoding texture colors into linear space is a common operation therefore the EXT_sRGB extension was created. Using this extension textures with sRGB data can be decoded for us on the fly even before sampling. As explained in The Importance of Being Linear this is preferred method:

The automatic sRGB corrections are free and are preferred to performing the corrections manually in a shader after each texture acces, because each pow instruction is scalar and expanded to two instructions. Also, manual correction happens after filtering, which is incorrectly performed in a nonlinear space.

I won't use it for now as it's not supported everywhere and I want to avoid automagic.

To enable this extension in WebGL you need to call:

var ext = gl.getExtension('EXT_sRGB')

Then when uploading texture data to the GPU we will use ext.SRGB_EXT instead of gl.RGB.

gl.texImage2D(gl.TEXTURE_2D, 0, ext.SRGB_EXT, gl.UNSIGNED_BYTE, ext.SRGB_EXT, data);

In pex we specify sRGB data when creating the texture. Context will check for the EXT_sRGB extension and enable it for us when available./

this.texture = ctx.createTexture2D(
   res.texture,
   res.texture.width,
   res.texture.height,
   { repeat: true, format: ctx.SRGB }
);

Then in our shader we can now skip toLinear call for the texture data

//sample color as usual, the RGB values
//will be converted to linear space for you
vec4 baseColor = texture2D(uAlbedoTex, vTexCoord0 * vec2(3.0, 2.0));
vec4 finalColor = vec4(baseColor.rgb * diffuse, 1.0);

//we still need to bring it back to the gamma
//color space as we don't have sRGB aware render buffer here
gl_FragColor = toGamma(finalColor);

To run the example:

beefy 206-gamma-ext-srgb/main.js --open --live -- -i plask -g glslify-promise/transform

According to WebGL ReportEXT_sRGB is supported in:

Additionally

If you don't have EXT_sRGB enabled or supported you will get brighter image than expected due to applying gamma to non-linear data (still in gamma space).


click to see the live version in a separate window

Uff, that's the end of Part 2. Next time we will talk about hight dynamic range (HDR) which is intro to Image Based Lighting ("the number 2" trick in PBR).

Comments, feedback and contributing

Please leave any comments below, on twitter @marcinignac or via positing issues or pull request on Github for this page pragmatic-pbr/200-setup-and-gamma.md.